Trigonometric Identities

4.3 -- Right Triangle Trigonometry

The Six Trigonometric Functions

There are three different lengths of a triangle. One is the side opposite theta, the second is the side adjacent theta, and the last is the hypotenuse (opposite of the right angle). The lengths of these sides can be used to determine the Six Trigonometric Functions which include:

Sine- Opposite/Hypotenuse

Cosine- Adjacent/Hypotenuse

Tangent- Opposite/Adjacent

Cosecant- 1/Sine or Hypotenuse/Opposite

Secant- 1/Cosine or Hypotenuse/Adjacent

Cotangent- 1/Tangent or Adjacent/Opposite

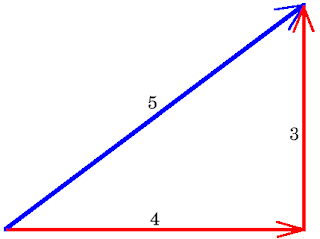
Here is an example of a right triangle, where "A" is theta.

Example:

Hyp-5

Opp-3

Adj-4

Given these numbers for the side lengths and the definitions above, we can find out any of these Six Trigonometric Functions like so:

Sin= 3/5

Cos= 4/5

Tan= 3/4

Csc= 5/3

Sec= 5/4

Cot= 4/3

The Basics of Trigonometry - 4.1

So what exactly is trigonometry?

Trigonometry is the measurement of triangles.
Well triangles have angles right? What are those you ask?

Angles are two rays with a common endpoint, which is called a vertex (plural--vertices). Every angle has an intial side, the starting position of the ray, and a terminal side, the position after rotation. Such an angle is in standard postion (see diagram to right). A positive angle is one that comes as a result of counterclockwise rotation. A Negative angle is one that results from clockwise rotation. Some of the angles that were discussed in class today are:

Acute - less than 90

Right - 90

Obtuse - greater than 90 but less than 180

Sraight - 180

Reflex - greater than 180

Complementary - (not to be confused with complimentary) - two angles whose sum is equal to 90

Supplementary - two angles whose sum is equal to 180

Since math always has to make things harder than they really need to be (just kidding Mr. Wilhelm...but not really), we no longer use degrees to measure angles; we use radians. But wait, what is a radian? One radian is the point at which the intercepted arc is equal to the radius of the circle. It can be represented by the simple equation s=r, where "s" is the intercepted arc and "r" is the radius.

Next, we talked about Coterminal Angles. Coterminal Angles are angles that have the same initial side and terminal side.

When changing from degrees to radians:

Multiply the degree measure by /180

When changing from radians to degrees:

Multiply the radian measure by 180/

Chapter 2 Section 4: Complex Numbers

Today we learned about Complex Numbers in Section Four.

Before we did that, though, we reviewed the realm of Real numbers. Real numbers include both Rational numbers (e.g. 4, -7, -7/3, 0), and Irrational numbers (e.g. ,  , 5+)

Next, Mr.Wilhelm started the section on complex numbers.  He described them as having a real part and an imaginary part.

Standard Form of a complex number:  a+bi (where a and b are both real numbers and i represents the imaginary).

We were reminded of the value of an imaginary unit:

                           i=

Addition and Subtraction of Complex Numbers:

When adding complex numbers, one treats the imaginary unit like any other variable.

                        (2+4i)+(6-5i)= 8-i

the same is true when subtracting..

                        (2+4i)-(6-5i)= -4+9i

Multiplication of Complex Numbers:

When multiplying complex numbers, the important thing to remember is that i^2= -1

                        (2+4i)(6-5i)=

                      12 +14i-20i^2=         you multiply -20 by -1 and get +20

                        12+14i+20=

                            32+4i

(always simplify and make sure your answer is in standard form)

Dividing Complex Numbers:

When dividing Complex numbers, the key thing to remember is to multiply the numerator and denominator of your problem by the conjugate of the denominator.

                         now multiply by the conjugate

next, distribute and get... 

next, simplify the i^2s to -1s...

next, combine like terms and get...

finally, convert into standard form...

After learning about operations of Complex Numbers, Mr.Wilhelm talked a little bit about how even if a graph (e.g. a parabola) does not touch the x-axis, it still has imaginary zeros.

Then, we talked about taking i to higher powers.

 i^1= i

i^2=-1

i^3= -i  (because root -1 times root -1 times root -1 is equal to negative root -1 which is equal to -i)

i^4= 1 (because root -1 times root -1 times root -1 is equal to negative root -1, and when you multiply that by another root -1 you get -i^2 which is equivalent to 1)

we also talked about how this applies to other higher powers in a cycle of fours but I don't really understand that yet so I probably shouldn't confuse all of you..

We finished off the day talking about imaginary numbers as zeros, converting the zeros into polynomials and vice versa.

*If something like 5+3i is a zero, then its conjugate (5-3i) is also a zero

Example (creating a polynomial out of zeros and imaginary zeros):

Zeros: 2, 5+3i, and therefore 5-3i

the long way is...

f(x)= (x-2)(x-(5+3i))(x-(5-3i))

=(x-2)(x-5-3i)(x-5+3i)

=(x-2)[x^2-5x+3ix-5x+25-15i-3ix+15i-9i^2]

=(x-2)[x^2-10x+25-9i^2]

=(x-2)[x^2-10x+25+9]

=x^3-10x^2+34x-2x^2+20x-68

=x^3-12x^2+54x-68

the shorter way is...

(starting from the second step of the last example)

f(x)=(x-2)(x-5-3i)(x-5+3i)

(x-5-3i) represents (a-b) and (x-5+3i) represents (a+b), and when you take (a-b)(a+b) you get a^2-b^2

so in actuality you have f(x)=(x-2)(x-5)^2 -(3i)^2 (because x-5 represents a and 3i represents b)

this simplifies to

f(x)=(x-2)(x^2-10x+34)

=x^3-10x^2+34x-2x^2+20x-68

=x^3-12x+54x-68

 

                   

Solutions to review

Answer key

Don't forget to check out Assignment 4 on your sheet for a nice overview of the kinds of problems you should be able to do.

Section 2.1 Quadratic Functions

Today we learned all the Quadratic Functions. We learned about the definition of a Quadratic function as well as identifying the vertex of a quadratic Function by completing the square.

Definition of a Quadratic Function:

Example:

Let a,b,and c be real numbers with a not equal to 0.
f(x)=ax^2+bx+c
This is a second degree polynomial function or a quadratic function.

Standard Form of a Quadratic Function:

f(x)=a(x-h)^2+k
This equation is written in standard form.
This form is great for sketchy what a parabola looks like because it identifies the vertex of the parabola as (h,k).

Identifying the Vertex of a Quadratic Function:

Example:
Describe the graph of 2x^2+8x+7 and identify the vertex.

Solution:
f(x)=2x^2+8x+7 Write the original function so you don't get confused
f(x)=2(x^2+4x)+ 7 Factor the 2 out of the x terms
f(x)=2(x^2+4x+4-4)+7 Now you have to use (b/2)^2. SO add and subtract 4 within the parentheses
f(x)=2(x^2+fx+4)-2(4)+7 Regroup Terms
f(x)=2(x+2)^2-1 Write the equation in standard form.

To find the x-intercepts solve the equation f(x)=ax^2+bx+c

On Thursday, we learned how to divide factors. First, we did long division, and then we did synthetic division.

Long division:
For both methods of division, we used the example of:
divided by x + 3

First, since there is no term to the third degree, you have to put in a placeholder for that term.

After you have put placeholders in for any missing degrees, you can then start solving the problem. The first step in solving is to take the divisor and see how many times it can go into the first term of the quotient.

Since it goes in x^3 times, you would multiply (x+3) by x^3, giving you an answer of (x^4 - 3x^3). You then subtract that answer from the first two terms in the quotient (x^4+0x^3). The fourth degree terms will cancel out, leaving an answer of -3x^3. You then drop down the -10x^2 and repeat the process until all terms are used.

When you are done, your answer should be:

In the last term of the answer, the 1 is the remainder. Instead of using the remainder like we've always learned (as in stating the answer then saying "remainder 1" at the end,) you must take the remainder and divide it by the divisor. The remainder will always go over the divisor.

Synthetic division is a shorter process that only works when the x term in the divisor is linear and has a coefficient of 1. Using the same equation as above, here is an example of synthetic division:

To start, you must take the coefficients of all the terms in the quotient (including placeholder terms) and line them up.

1  0  -10  -2  4

After doing so, drop down the first term- in this case, 1.

1  0  -10  -2  4

1

Next, multiply 1 by the divisor. Since the divisor is (x+3), you would multiply 1 by -3. This is because x = -3 when x + 3 = 0. Since 1 * -3 is -3, you would add that to the second term, or in this case 0.Your result would be -3, and you would drop that number below the 0.

1  0  -10  -2  4

1  -3

Next, you multiply the -3 under 0 by the -3 in the divisor to give you 9. You add 9 to the next term, -10, and you get -1. You place -1 under the negative term, and repeat this process until all terms have run out. Your result should be:

Again, the 1 is the remainder, which goes over the divisor, (x+3).

Another thing to remember is the rational root theorem.

f(x) = px^n + ... +q

The only possible rational roots are:
factors of p / factors of q

Therefore, if p = 3 and q = 7, then the only possible rational roots would be 1 or 3 divided by 1 or 7.

Section 2.2

Today we expanded a little on section 2.1 and began section 2.2.

The value of degree for a function is the maximum number of x-intercepts it can have.

First we touched up on some language and vocab that we would be using in the chapter.

• When referring to the highest possible point on a function, we use the word maximum. (Plural is maxima)

• When referring to the lowest possible point on a function, we use the word minimum. (Plural is minima)
• Both the maximum and minimum, when referring to both together, we use the term extreme points. (Plural extrema)

 As we looked at the value of degree in a function, we took note of some patters.

• The maximum degree of a function equals the maximum number of times that function can cross the x-intercept
• The maximum number of extrema (both maximas and minimas) equals one less than the highest degree of that function

 For example: If the highest degree of that function is 4, than the maximum number of extrema is 3. (4-1=3).

Than we looked at the end behavior of a function.

• If the x value increases and moves to the right, than   
• If the x value decreases and moves to the left, than
• If the y value increases and moves up, than 
• If the y value decreases and moves down, than

• If the maximum degree of the function is even, than the ends will move in the same direction
• If the maximum degree of the function is odd, than the ends will move in opposite directions

Than we talked about if were were given the zeros of a function, how we could find the function the were derived from.

Example: Zeros of the function are when x= -5, -1, 4

When x is -5 it means the (x+5)=0        When x is -1 it means that (x+1)=0
When x is 4 it means that (x-4)=0

So to write that as a function we just find the product of those three.
f(x)= (x+5)(x+4)(x+1) 
(And you can leave the equation like that for the most part, you won't be required to multiply it out)